Basic Numeracy Test
The numeracy test is the most basic numerical aptitude test and is designed to assess the testee's ability to manipulate basic mathematical concepts without the help of a calculator. This cognitive test assesses the candidate's ability to analyze mathematical problems and draw logical conclusions in a limited time.
A distinction must be made between two types of numeracy tests: the numeracy test and the numerical reasoning test. Learn more about these aptitude tests by consulting our guides or buying our complete package below.
Numeracy Test Pack
We have exclusively created the only simulation for the basic numeracy tests.
Included:
- Full simulation of 4 hours and 50 minutes.
- A total of 290 questions with answers, divided into 6 sections.
- Questions that can be presented as direct calculations or mathematical problems.
- 50 basic arithmetic questions including basic calculus operations (addition, subtraction, multiplication and division).
- 50 percentage questions.
- 30 questions of fractions.
- 50 unit conversion questions.
- 50 power questions.
- 50 number series questions (sequences of numbers).
- 10 geometry questions
- Tests are provided in PDF format for printing convenience.
- Complete introduction and study guide for each section, including a wide variety of rules, formulas and mathematical tricks.
- 10 exercises combining graphs and tables.
- Secure payment & FAQ.
The various numerical cognition tests generally comprise the following arithmetic concepts:
| Numeracy topics | |
|---|---|
| Percentages | Number series (sequences) |
| Basic calculation operations | Proportions and ratios |
| Fractions | Problems |
| Conversion of units | Equations |
| Exponents (powers) | Roots |
Percentages
A number is a percentage if it can be expressed as a fraction with a denominator of 100 or as a decimal. For example, a percentage of 30 percent can be expressed as following:
- 30 %
- 0.3
There are a number of need-to-know percentages:
- 100% corresponds to 1 or the entirety of the quantity in question.
- 50% corresponds to 0.5 or half.
- 25% corresponds to 0.25 or a quarter.
In order to calculate the percentage of a certain quantity, you must simply multiply it by the percentage, expressed as a fraction or as a decimal. For example, the method in which we calculate 30% of 80 euros is:
A typical percentage question example:
48% of the 725 students are girls. The number of girls is:
- 348
- 345
- 378
Answer
The correct answer is answer A.
Taking 48% of a quantity is equivalent to multiplying the amount by 0.48, so:
0.48 x 725 = 348 ou
Basic calculation operations
Addition
In order to add two (or more) numbers, the unit figures and the tens figures are added successively, taking into account a possible retention. The hundreds figures are then added, also taking into account any retention from the tens figures. The addition calculation is to be continued in the same manner, depending on the amount of figures in each number.
Example:

In order to add decimal numbers, you must first add the decimal numbers (to the right of the comma) and then the numbers to the left of the comma.
Example:
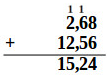
Subtraction
Example:

The multiplication
To multiply a number by 10; 100; 1 000; etc., add to the number as many zeros as the multiplier number has, or shift the comma to the right by as many digits as there are zeros in the multiplier.
Example:
25 x 10 = 250
75 x 1 000 = 75,000
12.25 x 10 = 122.5
To multiply a number by 5; 50; etc., divide the number by 2 and multiply the result by 10; 100; etc.
64 x 5 = (64 / 2) x 10 = 32 x 10 = 320
Therefore: to divide a number by 5; 50; etc., divide the number by 10; 100; etc., and multiply the result by 2.
64 / 5 = (64 / 10) x 2 = 6.4 x 2 = 12.8
To multiply a number by 0.05; 0.005; etc., divide the number by 2 and then divide the result by 10; 100; etc.
64 x 0.05 = (64 / 2) / 10 = 32 / 10 = 3.2
Therefore: to divide a number by 0.05; 0.005; etc., multiply the number by 2, then multiply the result by 10; 100; etc.
64 / 0,05 = (64 x 2) x 10 = 128 x 10 = 1,280
To multiply a number by 25, divide it by 4 and multiply the result by 100.
32 x 25 = (32 / 4) x 100 = 800
To multiply a number by 2.5; divide it by 4 and multiply the result by 10.
32 x 2.5 = (32 / 4) x 10 = 80
Therefore: to divide a number by 25, multiply it by 4 and then divide the result by 100.
32 / 25 = (32 x 4) / 100 = 1.28
To multiply a number by 101, 1001, etc., multiply the number by 100, 1,000, etc., and add the number to the result.
25 x 101= 2 500 + 25 = 2,525
In order to multiply a number by 9; 99; etc., you must simply multiply the number by 10; 100; etc. (depending on the number of digits), and subtract the original number from the result.
25 x 99 = 2500 - 25 = 2475
To multiply a number by 0.20, the number is divided by 5, following which, in correlation to the rule of multiplying by 5, the number is divided by 10 and the result is then multiplied by 2.
25 x 0.20 = 2.5 x 2 = 5
The division
| Division criteria | |
|---|---|
| Rule | Examples |
| A number is divisible by 5 if the number of units is 0 or 5. | 750/5 = 150 |
| A number is divisible by 3 if the sum of the digits is divisible by 3. | 534 → 5 + 3 + 4 = 12 |
| A number is divisible by 4 if the number formed by the last 2 digits is divisible by 4. | 1612, 54760,... |
| A number is divisible by 6 if it is divisible by 2 and 3. | 72/6 = 12 72/2 = 36 72/3 = 24 |
| A number is divisible by 9 if the sum of the digits is divisible by 9. | 84321 → 8 + 4 + 3 + 2 + 1 = 18 |
| A number is divisible by 10 if the number's last digit is a zero. | 532985920 |
| A number is divisible by 11 if the sum of its even number subtracted from the sum of its odd number is zero or a multiple of 11. | 13574 : 3 + 7 = 10 - (1 + 5 + 4) = 10 - 10 = 0 So 13754 is divisible by 11 |
| A number is divisible by 20 if it ends in 00-20-40-60-80. | 380, 40348260,... |
| A number is divisible by 25 if it ends in 00-25-50-75. | 525, 89504350,... |
Order of Operations
In mathematics, the order of operations is a collection of rules that reflect conventions that establish the order in which one must operate when seeking the value of a chain of operations.
The order is as follows:
- Parentheses (brackets) (P)
- Exponents (E)
- Multiplication and division (MD)
- Addition and subtraction (AS)
An easy way to remember this order is by way of the mnemonic PEMDAS.
Example:
28 – 3 (12 ÷ 4) – 4²
= 28 – 3 × 3 – 4²
= 28 – 3 × 3 – 16
= 28 – 9 – 16
= 28 – 25
= 3
Fractions
Components of a fraction
The fraction is composed of a numerator (a) and a denominator (b).
Equivalent Fractions
It is important to remember that there are several ways to represent the same fraction. For instance, fractions 1/2 and 2/4 are completely equivalent. How do we switch from one fraction representation to another, while maintaining equivalence?
A fraction remains equivalent if the numerator and denominator are multiplied or divided by the same number.
Example:
Simplification of fractions
A fraction can be written in simplified form if the numerator and denominator have no common factors. In other words, it is impossible to find a number that is a divisor of both the numerator and the denominator when a number is portrayed as simplified fraction.
Example
The fraction is not written in simplified form since there are numbers that both 120 and 200 are divisible by. The largest common divisor (factor) of 120 and 200 is 40, hence:
Since the numerator and denominator are divisible by the same number (40), the fraction is equivalent to
. In turn,
is the simplified form of
since no common division factor exists between 3 and 5.
Simplification can be achieved in several steps in cases where the greatest common factor between the numerator and the denominator is not easily recognized.
Example:
Fraction rules
| Subject | Rule | Example |
| Adding and subtracting fractions | ||
| The rule of addition and subtraction of fractions is only applicable if both fractions have the same denominator, which is not generally the case in numerical exams. The fractions must be converted into equivalent fractions with a common denominator. |
These fractions cannot be added together until they have been rewritten with a common denominator. The smallest multiple common of the numbers 3 and 5 is 15. 15 will therefore be the common denominator. | |
| Multiplication of two fractions | Unlike in the case of addition and subtraction, denominators do not need to be common in order to multiply fractions. | |
| Division of two fractions | This rule allows you to transform a division exercise into multiplication form, thus allowing for an easier solution. |
Useful tips:
Working with fractions does not change the priority of operations.
Example:
An integer can always be written as a fraction if an operation is to be performed between it and a fraction.
Example:
Avoid working with mixed numbers; transform them into simple fractions instead.
Example:
Conversion of units
Below are several tables representing the different units (length, mass, time, etc.).
Conversions by power of ten (multiples of one unit):
| Prefix | Tera | Giga | Mega | Kilo | hecto | centi | milli | nano | pico |
| Factor | 1012 | 109 | 106 | 103 | 102 | 10-2 | 10-3 | 10-9 | 10-12 |
Length units
| gigameter | gm | 109m | 1,000,000,000 m |
| megameter | Mm | 106 m | 1,000,000 m |
| kilometre | km | 103m | 1000 m |
| hectometre | hm | 102 m | 100 m |
| decametre | dam | 10 m | 10 m |
| metre | m | 1 m | 1m |
| decimetre | dm | 10-1 m | 0.10 m |
| centimetre | cm | 10-2 m | 0.100 m |
| millimetre | mm | 10-3 m | 0.1000 m |
| micrometre | µm | 10-6 m | 0.1000000 m |
| nanometre | nm | 10-9 m | 0.1000000000 m |
Mass units
| 1 ton | t | 106 g | 1,000,000 g |
| 1 kilogram | kg | 103 g | 1000 g |
| 1 gram | g | 1 g | 1 g |
| 1 milligram | mg | 10-3 g | 0.001 g |
| 1 microgram | µg | 10-6 g | 0.000001 g |
| 1 nanogram | ng | 10-9 g | 0.000000001 g |
Time measurement units
| 1 millennium | 1000 years |
| 1 century | 100 years |
| 1 decade | 10 years |
| 1 lustrum | 5 years |
| 1 year | 365 days |
| 1 week | 7 days |
| 1 day | 24 hours |
| 1 hour | 60 minutes ou 3,600 seconds |
| 1 minute | 60 seconds |
Area units
| km² | hm² | dam² | m² | dm² | cm² | mm² |
| 1,000,000 | 10,000 | 100 | 1 | 0.01 | 0.0001 | 0.000001 |
Conversion of surface and volume units
| 1 mm | 10-3m |
| 1 mm² | 10-6m |
| 1 mm³ | 10-9 m |
Powers
Laws of powers
Reminder:
a0 = 1
a1 = a
a - 1 = 1/a
an = a × a × ... × a (n factors)
a - n = 1 / an
Tip:
To save time during a numeracy test, we recommend you memorize the following chart:
| 0² = 0 | 5² = 25 | 8² = 64 | 11² = 121 | 14² = 196 |
| 1² = 1 | 6² = 36 | 9² = 81 | 12² = 144 | 15² = 225 |
| 4² = 16 | 7² = 49 | 10² = 100 | 13² = 169 | 16² = 256 |
Number series
Number series questions are frequently used in numeracy tests. They make it possible to evaluate the candidate's ability to understand numerical logic as well as to evaluate his or her potential to complete mental calculations.
The number series may combine several basic computational operations (addition, subtraction, etc.), or correspond to certain logic using the number properties (even, odd, first,...).
The following are examples of series that may appear in numeracy tests:
| General Series | Even number series | 2, 4, 6, 8, 10,12,... |
| Series of odd numbers | 1, 3, 5, 7, 9,11,13,... | |
| Prime numbers | 2, 3, 5, 7, 11 ,13,17,... | |
| Multiples of 3 (or any other number) | 3, 6, 9, 12, 15,18,... | |
| Arithmetic sequences a series of numbers where we move from one term to the next by always adding the same number | Continuation of reason 3 (i.e. +3) | 2, 5, 8, 11, 14, 17,... |
| Continuation of reason -3 (i.e. -3) | 17, 14, 11, 8, 5, 2,... | |
| Geometric sequences a series of numbers where we move from one term to the next by always multiplying by the same number | Continuation of reason 4 (i.e. +4) | 2, 8, 32, 128, 512,... |
| Suite de raison -4 (i.e. -4) | 512, 128, 32, 8, 2,... | |
| Series with operations between numbers | Addition of the previous number | 1, 2, 3, 5, 8, 13, 21,... |
| Follow-up | Two suites in one | 2, 3, 4, 6, 6, 9, 8, 12,10,... |
| Several operations | Following two operations (+3, x2) | 1, 4, 8, 11, 22, 25, 50,... |
| Following three operations (+2, x3, -1) | 1, 3, 6, 5, 7, 21, 20,... |
Proportions & Ratios
Proportions
Proportionality:In mathematics, two sets of numbers are said to be proportional when one can move from one to the other by multiplying or dividing the first by the same non-zero constant.
Rule of three or proportionality rule:This rule allows the calculation of a product from 3 given numbers, according to the following formula:
A simple example:
| Tomato weigh (kg) | 1 | 2 | 3 | 4 | 5 |
| Price | 2 | 4 | 6 | 8 | 10 |
The proportionality coefficient is 2.
Example of a test question:
| Carrier from "Kuehne + Nagel" | |||
| Trucks | Consumption Number of liters per 100 km | Number of km per day | |
| Container 20'' | Container 40'' | ||
| Truck A | 20 | 30 | 150 |
| Truck B | 17 | 21 | 120 |
| Truck C | 18 | 23 | 135 |
How many more litres of fuel does truck B consume with the 40'' container than with the 20'' container?
- 4,5
- 3,9
- 4,8
- 5,1
Answer
The correct answer is answer C.
In order to solve the question, it is first necessary to create an equation using the rule of three, in order to determine the number of litres consumed by truck B with the 20" container in one day:
Truck B therefore consumes 20.4 litres of fuel per day with the 20" container.
The same calculation must then be followed out for the 40" container:
Truck B therefore consumes 25.2 litres of fuel per day with the 40" container.
→ 25.2 litres - 20.4 litres = 4.8 litres
Ratios
A ratio is a quantitative relationship between two numbers that describes how many times one value may contain another. Ratios are used intuitively in everyday life, such as in cooking recipes, or to calculate the size of computer and smartphone monitors.
Conversion of the best known decimal numbers into ratios:
- 0.1 = 1;10 or 1 for 10
- 0.2 = 1;5 or 1 for 5
- 0.25 = 1;4 or 1 for 4
- 0.33 = 1;3 or 1 for 3
- 0.5 = 1;2 or 1 for $2
Example of a simple ratio exercise that may appear in basic numeracy tests:
In an engine, an oil-to-fuel ratio of 3;100 is required. If 200 ml of gasoline is poured into the engine, how much oil should be added?
- 8 ml
- 5 ml
- 6 ml
- 15 ml
Answer
The correct answer is answer C.
In this type of exercise, you may use intuition in order to answer the question, due to the fact that it is enough to double the values in order to find the right answer. In more complicated exercises, it will be necessary to perform a certain calculation to find the correct value.
More complex example:
What is the mortality rate ratio between the 1950s and 1990s?
| Year | Crude birth rate (%) | Crude mortality rate (%) | Natural growth rate (%) |
| 1950 | 20 | 24 | 5 |
| 1960 | 29 | 23 | 6 |
| 1970 | 31 | 21 | 10 |
| 1980 | 38 | 19 | 19 |
| 1990 | 47 | 18 | 29 |
- 2;3
- 4;3
- 5;6
- 2;4
Answer
The correct answer is answer B.
Answering the above question necessitates calculation in order to find the right answer. First, divide the two values of the requested mortality rates, i.e. 24/18, which is equal to 1.3333. In order to transform this fraction into a ratio (ideally, this conversation should be memorized by heart, as it is often used), the fraction must be multiplied by a certain number, in order to obtain an integer. So for this example: 1.3333 x 3 = 4, the ratio is 4:3, answer B.
Problems
A mathematical or quantitative problem is defined as a question that can be solved using the elements given in the statement. The questions generally consist of a set of information presented in various forms (text, table, drawing, etc.), and in order to be solved, require the use of mathematical concepts and/or tools.
In a numeracy test, the problem presented can usually be solved intuitively or with basic mathematical concepts as presented above.
Example:
Two trucks were driven over a distance of 1,680 kilometres (km). The first truck travelled an average of 14 km per litre of fuel during the trip and the second truck travelled an average of 12 km per litre. How many more litres of gasoline did the second truck consume than the first?
- 10
- 20
- 30
- 40
- It is not possible to say this with the information provided.
Answer
The correct answer is answer B.
In order to solve the problem, it is necessary to calculate the total number of litres used for each truck, and then calculate the difference between them.
Truck A : 1680/14 = 120
Truck B 1680/12 = 140
140 - 120 = 20, answer B.
Example 2:
A book is available at the local bookstore in digital version (eBook) for 5.90 Euros and paperback for 13.40 Euros. The book can also be obtained from Amazon with a 15% discount, plus 2.50 Euros for shipping costs. What is the price difference between the digital version and the paperback version ordered on Amazon?
- 8.14 Euros
- 9.83 Euros
- 6.99 Euros
- 7.45 Euros
- 7.99 Euros
Answer
The correct answer is answer E.
In order to calculate the price difference between the two book formats, it is first necessary to calculate the book price, whilst taking the discount and shipping costs into account.
13.40 x 15/100 = 2.01
13.40 - 2.01 + 2.50 = 13.89
13.89 - 5.90 = 7.99
Equations
What is an equation?
An equation is composed of both known numbers and one or more unknown values (number whose value is unknown), and information needed in order to calculate their value.
Example of a simple equation:
3x = x + 72
3x - x = 72
x (3 - 1) = 72
2x = 72
x = 72/2
x = 36
Transforming the equation into a verbal question may simplify understanding of the question. When transformed, the above equation reads: I am an unknown number. I am equal to one-third of my number plus 24. What am I?
Remarkable identities: Out of all the basic formulas that exist, there are three we highly recommend you learn, as they greatly facilitate certain calculations.
The first is: (a + b)² = a² + 2ab + b²
The second is: (a – b)² = a² - 2ab + b²
The third is: a² – b² = (a + b)(a - b)
These formulas can be applied in both directions.
Example: (2 + 3)² = 4 + 12 + 9 = 25
Root
Here are some summary tables concerning roots:
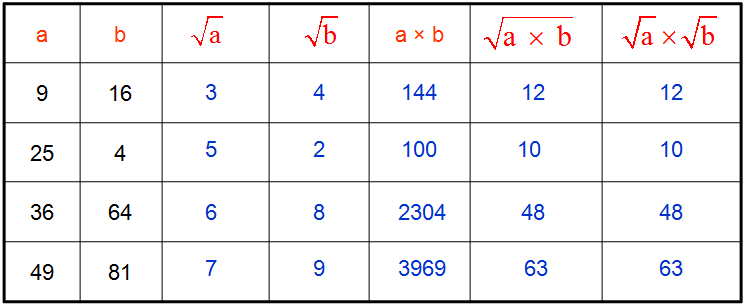
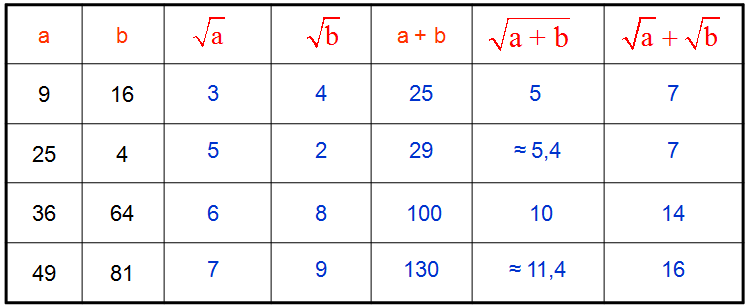
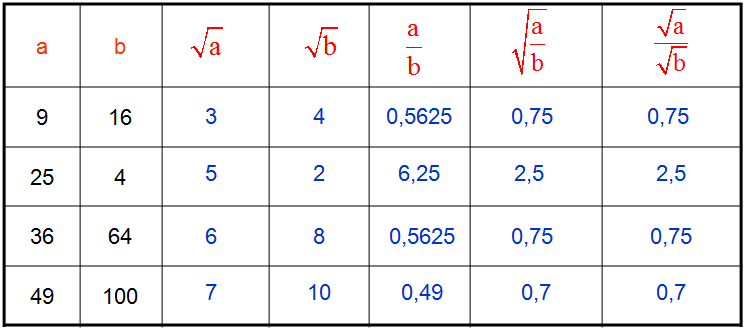
For which jobs is the numeracy test used?
The numeracy test is used for non-managerial positions requiring effective mental calculation skills in any situation, including jobs where the candidate is required to use his or her knowledge on a daily basis and under pressure. Examples of occupations requiring these skills:
- Sales-related professions
- Bus and train drivers
- Technical assistants (help desk support)
- Customer Services
- Nurses, midwives and paramedics
- Soldiers and other military personnel
- Steward and flight attendant
- Prison supervisor
- And many more.
The main publishers of numeracy tests
| Publishers | Tests |
|---|---|
| SHL | SHL Verify Checking & Calculation Tests |
| PSI Online / SHL | Math Problem Solving |
| cut-e | scales eql - Numeracy |
| Criteria | Criteria Basic Skills Test (CBST) |
| Wonderlic | Wonderlic Basic Skills Test (WBST) |
| Thomas International | Thomas International GIA |
| Saville Consulting | Administrative Numerical Comprehension |
| Saville Consulting | Customer Numerical Comprehension |
| Saville Consulting | Commercial Numerical Comprehension |
| Saville Consulting | Operational Numerical Comprehension |
| Criterion | B2C Numerical Ability Test |
| Criterion | CWS Numerical Ability Test |
| Selective Hiring | Basic Math Skills |
| HRdirect | SkillSeries Math Test |
| TAFE SA | TABE Numeracy Test |












