Logical Reasoning Test
The Logical Reasoning Test is one of the most popular forms of psychometric tests used during hiring processes.
What Is a Logical Reasoning Test?
The Logical Reasoning Test evaluates the candidate's logical abilities; his or her ability to draw logical conclusions from various situations presented to them. It allows employers to gain an impression regarding a candidate's ability to make decisions in a given time frame, as well as his or her ability to reason in a coherent and logical manner.
The Different Types of Logical Tests
The most prevalent logical reasoning tests used in recruitment processes and university admission tests are the following:
- Verbal logical reasoning
- Inductive reasoning
- Spatial reasoning
- Abstract reasoning
- Diagrammatic reasoning
- Matrices
Logical Reasoning Practice Test
Exclusively, we have created the logical reasoning simulation practice test.
The pack includes:
- A total of 228 questions.
- 25 verbal logical reasoning questions for 20-minutes, including many different verbal logic exercises (deductive reasoning, syllogisms, abductive reasoning, missing argument, arrangements).
- 12 inductive logical reasoning questions for 12-minutes.
- 30 diagrammatic reasoning questions for 13-minutes.
- 50 deductive logical reasoning questions for 30-minutes.
- 20 abstract reasoning questions for 8-minutes.
- 10 abstract reasoning questions with matrices for 3-minutes.
- 11 spatial reasoning questions for 5-minutes.
- 50 spatial visualization questions for 8-minutes.
- Answers with concise explanations for most sections.
- Tests are provided in PDF format for printing convenience.
- Secure payment & FAQ.
Below you will find further details about each of various logical reasoning tests, including free question examples:
Verbal Logic Reasoning Test
Verbal logic questions comprise an important part of reasoning tests, applicable to both verbal and logical reasoning tests. They can be adapted for use in exams requiring verbal skills or in tests combining different logical thinking skills, according to criteria chosen by employer/test editor/university.
Verbal logic questions may consist of various subtypes of logical reasoning:
Deductive Logical Reasoning Test
The deductive reasoning, or deductive logical thinking tests, involves drawing logical conclusions from various facts and statements.
In these types of exercises, the candidate must determine whether two (or more) sentences have the same meaning despite being presented or structured in a different manner.
In order to solve this type of exercise, it is possible to use your basic logic or "common sense". However, doing so has two major shortcomings: solving complex questions requires greater speed, and you are also very likely to encounter statements that are shocking, seemingly irrational or against your common sense, yet adhere to the fundamental rules of logic throughout.
For example, the sentence: "all rabbits run" is equivalent to the sentence "anything that doesn't run is not a rabbit". You will notice that, although the sentence seems strange in its own right, this does not mean that it is devoid of logic; the absurdity of this statement is only intended to confuse you.
In order to assist you with these kinds of problems, AptitudeTests.org advises the use of a certain technique called formal logic, or conditional syllogism. This method will allow you to systematize the exercises in a manner that allows for easier resolution. Our PDF simulation details all the steps of this method, enabling you to easily solve deductive reasoning exercises (amongst others) using simple and practical diagrams.
Examples of Deductive Logical Reasoning Question
The vast majority of swallows are blue. What is the most logical conclusion?
- There is a white swallow.
- Not everything that is blue is a swallow.
- There is a blue swallow.
- None of the answers are satisfactory.
Answer
The vast majority of swallows are blue so the answer must be C: there is a blue swallow.
Syllogism
Syllogism is a type of reasoning invented by Aristotle, entailing the deduction of a third proposition from two given ones, thus linking three assertions or arguments. Two of them are called "premises” since they lead to a "conclusion". The two premises can also be divided.
- The major premise is considered to be the most general assertion.
- The minor premise can be defined as the least general statement.
The conclusion, on the other hand, is the inferred consequence of the two premises and may be legitimate or illegitimate. A conclusion is illegitimate when, even though the premises are true, the conclusion is not consistent with the first two statements' assertions.
Example of Syllogism Question
All humans are mortal.
Peter is human.
Therefore, Peter is mortal.
Useful information:
If the statement presented includes a subject which is part of a "majority" group, the conclusion cannot be presented as a statement about the group as a whole. Similarly, the entire group cannot be cited as a conclusion when the statement presented relates to a specific subset of the group.
The Missing Argument
This type of exercise is composed of a deductive reasoning exercise's partial conclusion (syllogism for instance), as well as its first argument. The purpose of the exercise is to find a second argument which will lead to the proposed conclusion.
The formal logic method explained in our Logical Reasoning PDF can also be used in order to solve missing argument questions.
Example of The Missing Argument Question
All rabbits are dogs. What additional information would be enough to conclude that all rabbits can swim?
- All dogs are rabbits.
- Anything that can swim is a dolphin.
- Anything with two legs can swim.
- All dogs can swim.
Answer
The correct answer is answer D: All dogs can swim.
Abductive Logical Reasoning
Abduction, also called abductive reasoning, consists of a series of arguments followed by a conclusion. The purpose of the exercise is to determine whether the conclusion flows from all, some, or none of the arguments.
This type of exercise begins with an assertion or a sequence of actual observations (A1, A2, A3, etc.), based on a probable basis (B) that can be taken as a hypothesis to affirm that it is the cause of said observations (A1, A2, A3, etc.) or of one of them in particular.
Abductive reasoning does not lead to an implicitly true conclusion, but rather allows for the presentation of logical hypothesis which can then be verified through further investigation.
This translates into the following logical framework:
- If A1, A2, A3, etc. are true.
- And if B is true, and this results in A1 being true, A2 being true, A3 being true, etc.
- Then B is true.
Example of Abductive Logical Reasoning Question
When it rains there are puddles in the street.
Molly sees puddles in the street.
She therefore infers that it rained.
This type of reasoning is probably the most difficult type of logical reasoning due to the ambiguous nature of the statement's conclusion. The best way to prepare for these type of exercises is to become familiar with the logical principles of the questions and problems presented.
Arrangements
In this type of exercise, situations and rules govern different possibilities for placing (or moving) people or objects.
The rules are often prohibitions or obligations, for instance, it is forbidden to place person x in a certain place or, on the contrary, it is compulsory to do so.
The strategy we recommend is to draw (by hand) a simple diagram based on the information presented to you in the statement.
Example of Arrangements Questions
Annie, Mary, and Diana are three sisters of different ages. Whenever they are asked their names, each one states either her own name or the name of an older sister. On one occasion, when all three were asked their names, two of them answered "Annie".
What is not possible?
- Diana is the middle sister.
- Mary is the older sister.
- Annie is the younger sister.
- Mary is the middle sister.
Answerr
The correct answer is answer C: Annie is the youngest sister.
Spatial Reasoning Test
Spatial reasoning is one of the most popular types of logic exercises. It is used to analyze the candidate's spatial abilities i.e. his or her ability to connect different objects in two or three dimensional space, to flip them, to fold them, or to imagine a sequence that could correspond to different abstract forms arranged in a precise order.
There are many components of spatial reasoning tests. For more information on the different kinds of exercises and to see many more free examples, please visit the dedicated webpage.
Abstract Reasoning Test
The abstract/diagrammatic reasoning test assesses a candidate's or employee's ability to interpret or detect relationships between certain elements.
In many ways, this test is reminiscent of the IQ (intelligence quotient) test, both using the same type of reasoning. A test of abstract logic generally involves sequences of diagrams and geometric shapes repeated or modified in a logical order and therefore does not require prior knowledge, nor does it include numbers or texts. It is used to judge an employee's potential and further development. The questions in this type of test are generally similar to spatial reasoning exercises.
Odd-One-Out
"Odd-one-out" question types are very common in abstract reasoning tests. They generally consist of a series of figures, the number of which varies according to the specific test being taken. You must find the unique element among all others, i.e., the element that breaks the rule or that is unrelated to the others. As with the sequence of figures questions, one or more rules exist to help you perceive the order and arrangement of the elements. Odd-one-out questions can be of varying levels of difficulty, ranging from very simple to extremely complicated. Some tests are composed of questions that increase in levels of difficulty, such as the cut-e ix scale.
Example of a cut-e scales ix question
Who is the odd-one-out?

Answer
Element G constitutes the exception and is therefore the correct answer.
Find more information about this test on the next page.
Example of an Abstract Reasoning question (cut-e scales clx)

In the above cut-e (Aon) abstract reasoning exercise, two grids containing colored symbols and following a common rule are presented. In the block on the right, four additional grids are presented. The candidate must find the two grids that follow the same rule out of these four options.
Answer and explanation
In this example, it is easy to see that the rule governing the two grids on the left is: blue triangles are present in each of the two bottom lines. This rule is followed in the two grids on the right.
Inductive Reasoning Test
The inductive reasoning or inductive-logical thinking test is based on specific and limited observations, which may lead to general conclusions by way of fact analysis. However, unlike deductive and abductive reasoning, inductive reasoning is not based on verbal statement and is, more often than not, based on sequences of images and graphical forms whose order is predictable.
The inductive-logic test is one of the most popular logical reasoning tests used by employers and assessment centers. Successful completion of an inductive reasoning test demonstrates strong conceptual and analytical thinking skills.
Example from SHL
Which element completes the series?
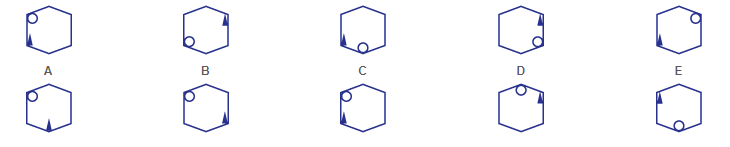
Answer and explanation
The correct answer is answer D.
In this example, there are two rules to be applied. The first is that the circle moves counter-clockwise in the hexagon. It follows that, in the following diagram, the circle will be in the upper corner of the hexagon, pointing to D as the answer. To confirm this, the second rule can be applied, according to which the position of the black triangle alternates between bottom left and top right. Thus, in the following diagram, the black triangle will need to be in the upper right corner of the hex. The answer is therefore definitely D.
Matrices
Matrices are part of spatial reasoning exercises that can be considered more complex than those presented above. A matrice may consist of nine or twelve elements, depending on the specific test. They are usually several logical sequences combined in a single exercise and these are typically composed of elements following each other horizontally or vertically.
In matrices exercises, one of the elements is replaced by a question mark. The aim of the exercise is to discover the figure that is supposed to be in that place, following the rules and logic governing the other sequences of the same matrice.
Example of a Spatial Reasoning Question with Matrices
The following matrice shows three sequences of figures from left to right:
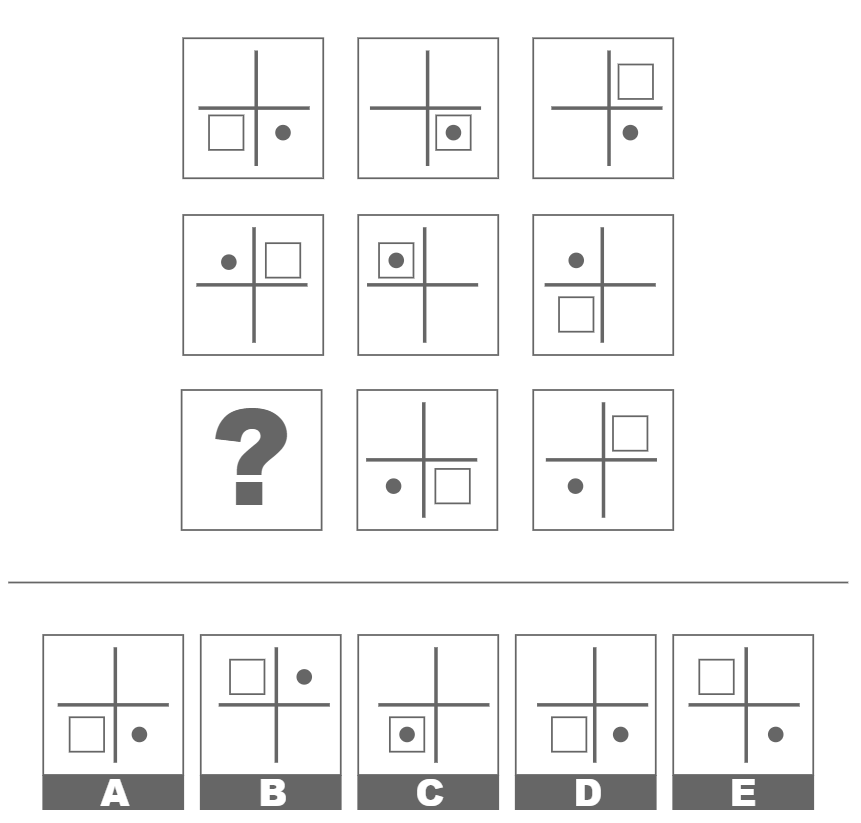
Answer and explanation
- The dot is constantly found in each of the three sequences but the square moves one square each time (to the right or left).
- In the third sequence, we can see that the square moves to the right, leading to the conclusion that the missing figure is found in answer C.
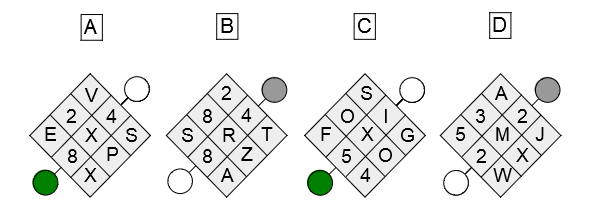
Example of an Inductive-logical Thinking (cut-e scales cls) Exercise
In the following cut-e scales cls exercise (discovery of roles and interrelationships), six diagrams are presented, each belonging to either the green or grey category. Each category has a common rule. Your task is to determine the category for each of the four diagrams below.
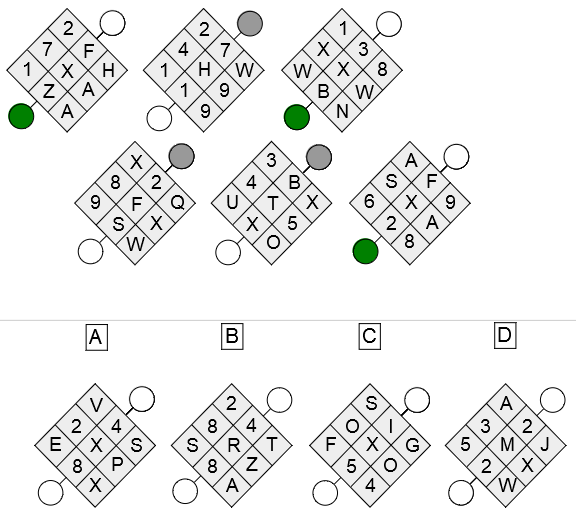
Answer and explanation
It is possible to establish very quickly that the green category diagrams all have an X in their center. This information is sufficient to separate the two categories and thus solve the exercise. Diagrams A and C therefore belong to the green category, whilst diagrams B and D belong to the grey category.
Diagrammatic Reasoning Test
Diagrammatic reasoning questions may appear in different forms. In the following example, the diagram is composed of different types of figures, called "basic figures" and "final figures". The basic figures are located in a square at the base of the arrows, whilst the final figures appear at the end of the arrows and are also surrounded by a square. Between these two types of figures, one or more functional figures (round with a shape inside) can be found, determining which transformation is applied to one or more of the basic figures. Your task is to compare the basic figure(s) with the final figure(s) and determine the effect of each function. Next, you must answer the questions that appear after each screen.
Example of a Diagrammatic Test Question
Which of the proposals A, B, C or D completes the diagram?
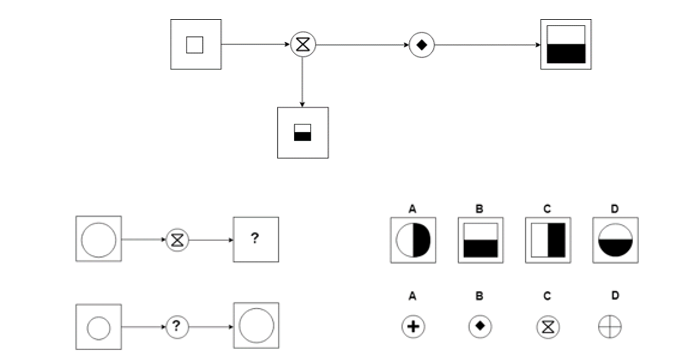
Answer and explanation
The small square is replaced by a large square split in half, the bottom half of which is colored black (final figure number 1):
Final figure number 2 designates a small square, the bottom half of which is also colored.
For both the two basic figures, the lower part of the figure has therefore been colored black whereas the size has only been modified for the basic figure number 1. Since the common function figure is the hourglass, it can be deduced that its function is to color the lower half in black. Therefore, the diamond function must change the shape size.
Consequently, the correct answer regarding the basic figure's appearance is answer D: the basic figure is a white circle. The function figure is that of the hourglass, whose function is to color the bottom half of the figure in black. Indeed, the final figure in D is a circle whose bottom half is colored black.

Regarding the functional figure, the correct answer is answer B: the basic figure is a small white circle whereas the final figure is a large circle. This is a result of the diamond figure; whose function is to enlarge the shape.
Useful information:
It is necessary to practice solving as many inductive reasoning questions as possible before taking the test. Inductive reasoning questions follow logic that can be assimilated and therefore identified much more quickly by practicing similar questions. The most common forms of inductive reasoning tests are sets of two forms (A and B), matrices, odd-one-out series, and symmetrical form sequences.
Tips and Tricks for Succeeding in Logical Reasoning Tests
- The best way to pass your logical reasoning test is to practice the different types of exercises you expect will appear in the exam, based on the reasoning exercises we have presented here. To help practice in a more comprehensive manner, and in order to maximize your chance of succeeding in the exam, AptitudeTests.org offers you a complete PDF simulation, created specifically to help you in your recruitment process.
- In addition, it is recommended to practice by varying means during your day-to-day, with the aim of improving your logical reasoning skills. For example, you could practice solving puzzles, logic games, riddles, etc.
- Analyze information presented in the form of diagrams or logical sequences such as those that you may come across in newspaper articles.
- Assemble your own furniture kits, following the diagrams and instructions in the manual.
Logical Reasoning Tests Used by Employers in Recruitment Processes
| Test Publishers | Assessment Tools |
| Assessio | Matrigma |
| SHL | Verify G+ |
| SHL | Verify Deductive Reasoning |
| SHL | Verify Inductive Reasoning (2014) |
| SHL | Verify Inductive Reasoning (2007) GU/MP |
| cut-e (AON) | scales cls - Inductive-logical Thinking |
| cut-e (AON) | scales clx - Inductive-logical Reasoning |
| cut-e (AON) | scales ix - Inductive-logical Thinking |
| cut-e (AON) | scalex fx - Deductive-logical Thinking |
| cut-e (AON) | scales lst - Deductive-logical Thinking |
| cut-e (AON) | scales sx - Deductive-logical Thinking |
| cut-e (AON) | scales mem - Spatial Memory |
| cut-e (AON) | scales nav - Sens of Navigation |
| cut-e (AON) | scales ndb - Spatial Orientation |
| cut-e (AON) | scales spc - Spatial Reasoning |
| cut-e (AON) | scales spr - 3D Spatial Reasoning |
| Thomas International | General Intelligence Assessment (GIA) |
| The Predictive Index | PI Cognitive Assessment (PI CA, PLI ou PI LI) |
| Cubiks | Logiks General Abstract (Intermediate) |
| Cubiks | Logiks General Abstract (Advanced) |
| Pearson TalentLens | Watson-Glaser Critical Thinking Appraisal |
| Talent Q (Korn Ferry / HayGroup) | Element Logical |
| IBM Kenexa | CAT Logical Reasoning Test (LRT) Logical Reasoning - Classifying Logical Reasoning - Decision Making Logical Reasoning - Drawing Conclusions Logical Reasoning - Deduction Logical Reasoning - Mathematical U.K. Logical Reasoning - Deduction U.K. Logical Reasoning - Mathematical |
| Siena | Siena Reasoning Test (SRT) |
| Thalento | SCOPE-test |